In order to
reconstruct a ionizing particle
trajectory, e.g. in High Energy
Physics Experiments, it is
needed to detect the positions
of this particles within the
space. The technique used for
this purpose consists on the
interposition along the trajectory
of several sensors planes
which are capable to detect the
positions where the particles
pass through; from the
interpolation of all these
points can be reconstructed the
trajectories followed by the
particles. In these environments
one of the most important merit
figure of the sensors is the spatial
resolution, that is
the capability to reconstruct
the crossing point of the
particle.
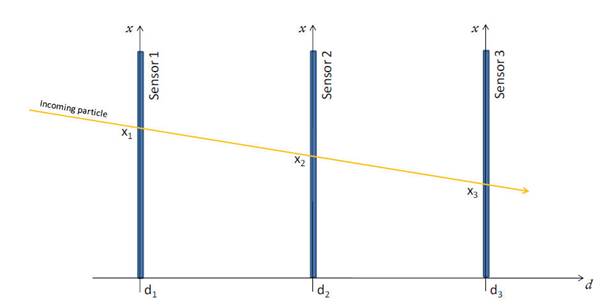
Fig. 1
Illustration of a tracking
system with three sensors
aligned one in front of each
other.
Basically,
the evaluation of the spatial
resolution of a particle sensor
consists on the irradiation of
the sensor under test with
particles beam at high energy
and on the measurement of the
differences between the measured
impact points with the real
ones. It is clear that it is
necessary to know the real
impact points of the incoming
particles, a solution of this
problem is to use a known
tracking system (usually
called telescope)
with which it is possible to
measure this positions. However
a solution that uses only the
sensors under test can be used.
We can use the same sensors for
which we want to measure the
resolution to track the
particle. The Figure 1
illustrates schematically this
system. For simplicity
considering a one-dimensional
system we can use at least three
sensors to detect the coordinate
x1, x2 and x3 of the particle
trajectory at three different
position d1, d2 and d3, from the
interpolation of two of these
points we can reconstruct the
particle path and use them to
estimate the position on the
third sensor. From simple
geometry considerations, if a
and b indicate the two sensors
used to estimate the position on
the third one, that is c, such
predicted position will be:
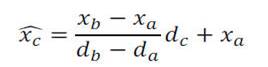
and the difference whit the measured one (in the following called residue also) mathematically is
:
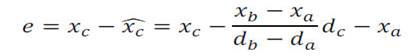
If we assume
that the uncertainty in the
position measurement has a
Gaussian probability density
function whit a standard
deviation σ,
e has a Gaussian probability
density function in turn with a
deviation of:
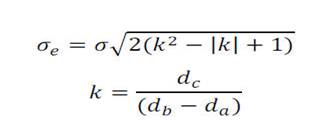
So, from the
standard deviation of e and
knowing the geometry of the
system it is possible to
retrieve σwhich
is the spatial resolution of the
sensors.
The previous
example however represents an
ideal case; in real cases there
are several sources of
uncertainty. Each sensor has a
non negligible thickness which
produces a deflection of the
incoming particle due to the
phenomenon of multiple
scattering.
The effect of multiple
scattering is to add another
aleatory contribution to the
coordinates of the measured
position. The effect on the
residues is to enlarge its
distribution; calling σs the
deviation introduced by the
multiple scattering we can make
the approximation:
where σr is
the real resolution.
Other sources
of uncertainty come from a non
perfect alignment of the
different elements. Each sensor,
as a solid body, has six
different degree of freedom,
namely three translations and
three rotations. The two
translations perpendicular to
the particles direction adds an
offset to the coordinates of the
impact point. The effect on the
distribution of the residue is
only a shift of the Gaussian
peak. The translation along the
particle direction adds an
uncertainty to the coordinate d,
however if the distance of a
sensor to another is big
compared to the position
uncertainty this component can
be neglected.
|
|
||
|
|
|
|
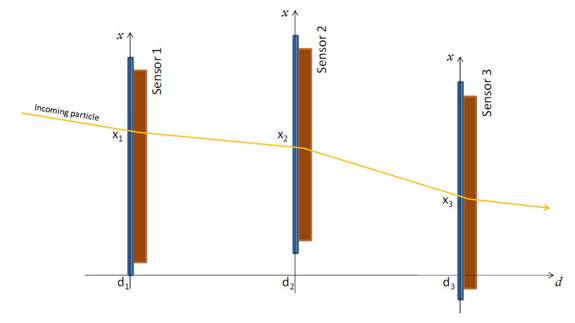
Fig. 2
Effect of the multiple
scattering and
misalignments in the detection
of a particle trajectory.
The rotations
(Figure 3) are more difficult to
compensate. Referring to the
Figure 4 a rotation around thex or y axis
has the effect shown in Figure
4(a), mathematically:
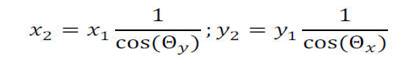
if the angles
are little (few degrees) the
correction can be neglected. For
the θd tilt
the situation is little more
complex because each coordinate x or y of
a sensor is related to both the
coordinates of another sensor
(see Figure 4(b)).
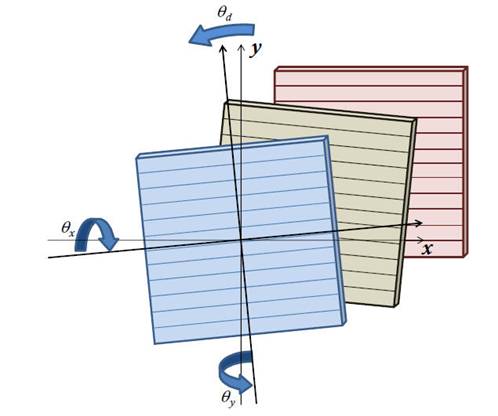
Fig. 3 The
three tilt angles among the
sensors.
Mathematically the tilt around
the axis parallel to the
particles beam direction can be
modelled as:
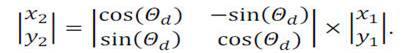
The effect of
all the rotation on the residue
is to widen its distribution,
but from the analysis of the
coordinate x2 and y2 detected
on a sensor as a function of the
coordinate x1 and y2 detected
to another sensor the tilt can
be estimated and corrected.
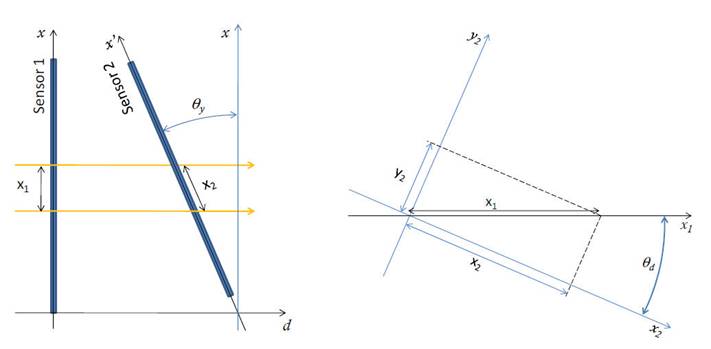
Fig. 4 Effect
of a non parallelism among two
different sensors.
Summarizing
the relation among two different
sensors we can consider:
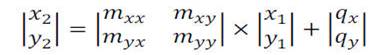
From the
measured points, using a
multiple linear regression
algorithm, it is possible to
retrieve the coefficients m and q.
Another
source of uncertainty comes from
the algorithm used to define the
crossing point of the particles
with each single detector. In
order to improve the resolution
in the position reconstruction,
it is possible to exploit the
charge sharing effect among
adjacent pixels. Usually the
barycentre algorithm is used (calledCOG,
Center Of Gravity).
Mainly due to the finite nature
of the detector and the
dimensions of the cluster the
COG, even if it allows to reach
lower resolution limit (i.e.
better resolution) than the
pixel dimension, it adds a
systematic error also.
References
-
D. Passeri et al., Characterization
of CMOS Active Pixel Sensors for particle detection: beam test of the four
sensors RAPS03 stacked system, Nucl.
Instr. and Meth. A 617 (2010) 573–575
-
D.Passeri,et al. Tilted
CMOS Active Pixel Sensors for Particle Track Reconstruction, IEEE
Nucl. Sci. Symp. Conf. Rec. NSS09 (2009) 1678. July 2006.
-
S. Meroli et al. A grazing angle technique to measure the charge collection efficiency for CMOS Active Pixel Sensors, Nucl. Instr. and Meth. A (2010), doi:10.1016/j.nima.2010.12.122
-
D. Biagetti et al. Beam
test results for the RAPS03 non-epitaxial CMOS active pixel sensor,
Nucl. Instr and Meth A 628 (2011) 230–233
| If you like... share with your friends |
