Multiple scattering is a phenomenon in which particles interact with matter and undergo multiple collisions with atoms or molecules. This process is important to understand in order to accurately model the behavior of particles in matter.
Considering that usually nuclei have mass greater than the incoming particle, the energy transfer is negligible but each scattering centre adds a small deviation to the incoming particle’s trajectory also.
Even if this deflection is small the sum of all the contribution adds a random component to the particle’s path which proceeds with a zig-zag path (see Figure 1.). As result, incoming beam after a thickness of material shown a divergence greater than the initial.
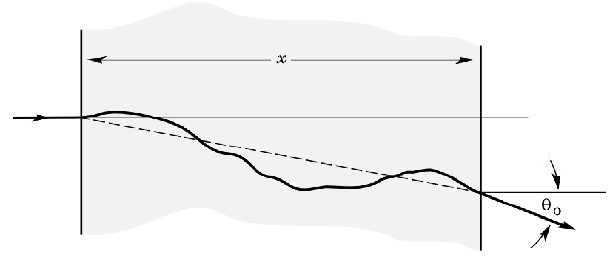
Fig 1. Effect of Multiple Coulomb Scattering.
Three situations can be considered:
1 - Single scattering.
Single scattering is a type of scattering that occurs when a particle interacts with a single target particle. This type of scattering is most common when the thickness of the target particle is extremely small, and the probability of having more than one interaction is negligible. The Rutherford formula is a mathematical expression that describes this type of scattering. The Rutherford formula is based on the assumption that the scattering is elastic, meaning that the energy of the incident particle is conserved during the scattering process.
The formula takes into account the charge of the incident particle, the charge of the target particle, the distance between the two particles, and the angle of scattering.
Practical examples of single scattering include the scattering of electrons off of atoms, the scattering of neutrons off of nuclei, and the scattering of photons off of electrons. In each of these cases, the thickness of the target particle is extremely small, and the probability of having more than one interaction is negligible.
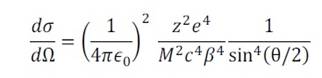
2 - Plural scattering.
When the number of Coulomb scattering increases but remains under few tens of interactions. This is the most difficult case to deal with, several works have been done by different authors (see [1] for further information)
3 - Multiple scattering.
When the thickness increases and the number of interactions become high the angular dispersion can be modelled as Gaussian.
Referring to multiple scattering, that is the most common situation, naming Θ the solid angle into which is concentrated the 98% of the beam after a thickness X of material, if we define Θ0= Θ/√2 as the projection of Θ on a plane, the angular dispersion can be calculated by the relation:
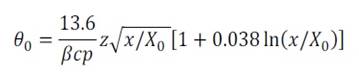
where p is the momentum and Xo is the radiation length. This last quantity is characteristic of the material and can be found tabulated by Y.S. Tsai [2] or can be used the approximated formula
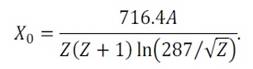
Applications of multiple scattering include particle accelerators, medical imaging, and nuclear physics. In particle accelerators, multiple scattering is used to control the trajectories of particles and to measure the properties of particles. In medical imaging, multiple scattering is used to create images of the body and to detect and diagnose diseases. In nuclear physics, multiple scattering is used to study the structure of nuclei and to understand the interactions between particles. Multiple scattering is also used in other fields such as materials science and astrophysics.
Modeling multiple scattering is challenging due to the complexity of the process and the limitations of existing techniques. The complexity of the process arises from the fact that the particles interact with the target material multiple times, resulting in a complex set of interactions. Additionally, existing techniques are limited in their ability to accurately model the behavior of particles in matter. As a result, researchers are continually developing new techniques to better understand and model multiple scattering.
References
-
E. Keil, E.Zeitler, and W. Zinn, Zeitschrift f r Naturforschung A, vol. 15A, no. 1031, 1960.
-
Yung-Su Tsai, Pair production and bremsstrahlung of charged leptons, Reviews of Modern Physics, vol. 46, no. 815, 1974
-
S. Meroli "Interaction of radiation with matter: from the theory to the measurements"


Anything missing? Write it here